modelicaでタイマー設定のヒーターをモデリングする

物理モデリングに優れた言語modelicaを使用して物理モデルと制御モデルが一体になったシミュレーションをします。

今回は以下の例題を参考にしながらすすめていきます。 mbe.modelica.university

以下のような制御をシミュレーションしてみます。

高温（温度T[K]）の物体Aが温度Tamb[K]の環境下に置かれている。
物体Aの温度Tはニュートンの冷却法則に従って低下していく。
物体Aの温度をコントロールするためのヒーターを設ける。
ヒーターは、物体Aの温度が設定値（Tbar + 1 [K])を下回った場合にONする。
ヒーターは、ONしてから設定秒(settime[s])経過したらOFFになる。

modelicaの実装

コードは以下のようになります。

model HysteresisControlWithAlgorithms "Control using algorithms"
  type HeatCapacitance=Real(unit="J/K");
  type Temperature=Real(unit="K");
  type Heat=Real(unit="W");
  type Mass=Real(unit="kg");
  type HeatTransferCoefficient=Real(unit="W/K");
  Boolean heat "Indicates whether heater is on";
  parameter HeatCapacitance C=1.0;
  parameter HeatTransferCoefficient h=2.0;
  parameter Heat Qcapacity=25.0;
  parameter Temperature Tamb=285;
  parameter Temperature Tbar=295;
  parameter Integer settime = 1 "Heater stop time";
  Integer count;
  Temperature T;
  Heat Q;
initial equation
  T = Tbar+5;
  heat = false;
  count = 0;
equation
  Q = if heat then Qcapacity else 0;
  C*der(T) = Q-h*(T-Tamb); 
algorithm
  when T<Tbar-1 then
    heat :=true;  
  end when;
  
  when heat and sample(0,0.1) then
    count := pre(count)+ 1;
  end when;
  
  when count/10 >= settime then
    heat :=false;
    count :=0; 
  end when;

解説

変数宣言部分は省略します。

initial equation
  T = Tbar+5;
  heat = false;
  count = 0;

各変数の初期値を設定しています。Tbarはパラメーターで値は295Kなので、温度Tの初期値は300Kですね。

equation
  Q = if heat then Qcapacity else 0;
  C*der(T) = Q-h*(T-Tamb);

物理モデリング部分です。

Q = if heat then Qcapacity else 0は、ブーリアン変数heatがtrueの時(ヒーターがONの時）Qcapacity(25 W)の熱が供給されるが、そうでない場合は０ということです。

C*der(T) = Q-h*(T-Tamb)はニュートンの冷却法則の式です。

algorithm
  when T<Tbar-1 then
    heat :=true;  
  end when;

離散制御の部分はalgorithmセクションで実装しています。離散制御は方程式よりも代入式で記述したほうが容易なためです。シミュレーション速度は低下するようですが。上記コードは

物体Aの温度Tが Tbar -1 K を下回った瞬間に、ヒーターがON（heatにtrueを代入する）

という意味になります。whenはその条件がoffからonになった1度のみ実行されます（その後、条件がoffに戻った時は、ONになった際に再度実行されます）。

when heat and sample(0,0.1) then
    count := pre(count)+ 1;
  end when;

上記はヒーターの起動秒数をカウントしています。 sample(0,0.1)は0秒時にtrueになり、それから0.1秒毎にtrueになります。グラフにすると以下のようになります。 f:id:Otepipi:20190817200322p:plain

そしてcountは「heat = trueかつsample(0,0.1)=true」のとき、自身に１を追加していきます。つまりこのcountの値が10になったとき、シミュレーション時間で1秒が経過したことになります。

 when count/10 >= settime then
    heat :=false;
    count :=0; 
  end when;

最後のブロックになります。「countの値の1/10（秒の次元）がsettime（1秒）以上になった瞬間に、ヒーターをOFFにする（heat=off)および秒数カウントをゼロに戻す」内容になります。

シミュレーション結果

シミュレーションの結果、各変数の挙動は以下のようになります。シミュレーションはOpenModelica v1.14で実施しました。

物体Aの温度T

f:id:Otepipi:20190817201133p:plain

温度が設定値まで下がるとヒーターが1秒間起動して温度上昇～を繰り返します。

ヒーターが与える熱量Q

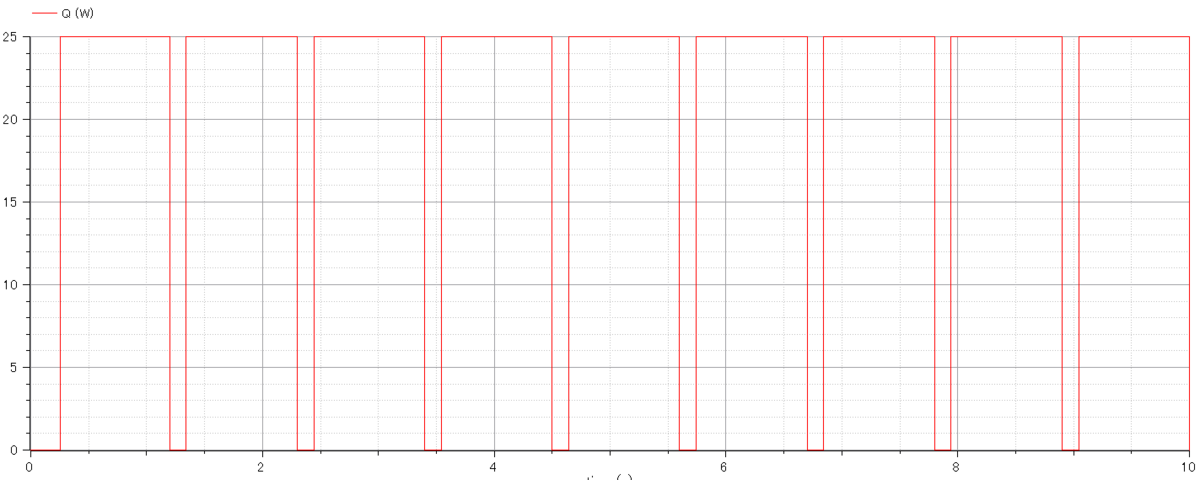f:id:Otepipi:20190817201227p:plain 離散的な挙動を示しています。

ヒーターの起動時間count

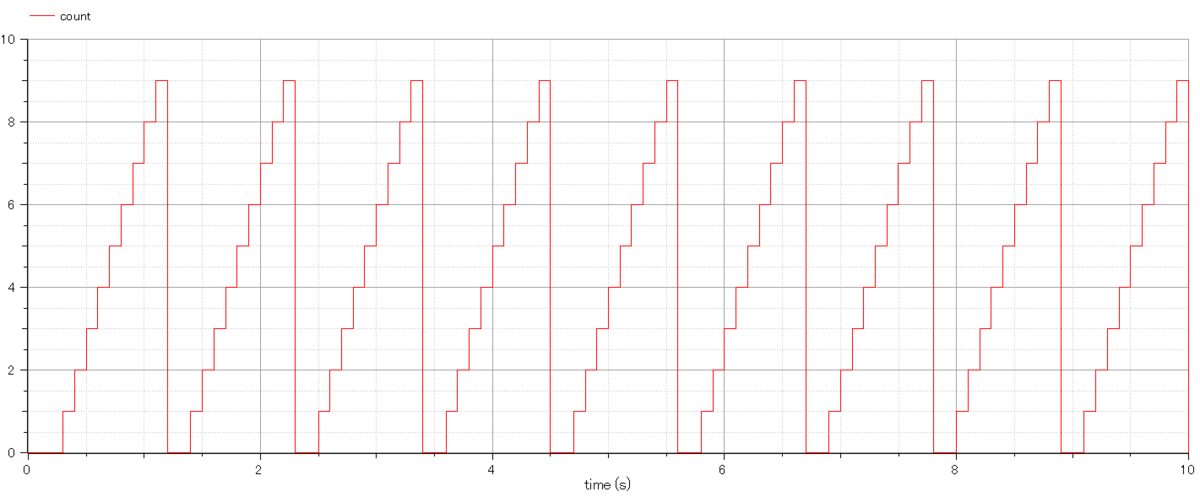f:id:Otepipi:20190817201414p:plain タイムステップの関係で1秒きっかりではありませんが、それなりの時間制度で離散制御できています。

こういった物理モデル（連続時間）と離散制御モデルを組み合わせたシミュレーションは一般的なプログラミング言語だとなかなか難しいのですが、modelicaでは労力少なく実装できます。modelicaは非常に面白い言語だと思いますので、今後も発信を続けていきたいと思います。

タイマー挙動の実装についてはこれは一例にすぎず、他の人の例を見たわけでもないのでもっと効率的な実装がありそうです。ご存知の方は教えて頂ければ幸いです。

今回はここまでにします。

システムとモデリング

modelica, Julia, Design Structure Matrix, SysML, 他モデリング全般について。