【Julia言語入門】Juliaとmodelicaで倒立振子のアニメーション

今回もJuliaとmodelicaの連携記事になります。

倒立振子のモデル

倒立振子のモデルはwikipediaにある台車駆動形倒立振子を使用します。

ja.wikipedia.org

f:id:Otepipi:20210211201525p:plain — wikipediaより引用

台車駆動形倒立振子の運動方程式は以下のようになります。

f:id:Otepipi:20210211203034p:plain

f:id:Otepipi:20210211201740p:plain

この式をmodelicaでシミュレーションします。この式は系全体を考慮するラグランジュ方程式から導出されたもので、オブジェクトベースのmodelicaを使用する意味は少ないのですが、modelicaは常微分方程式が書きやすいので今回使用してみます。

modelicaファイル

ファイルInvertedPendulum.moに以下を記述します。

package InvertedPendulum
// Package for simulating


    model Pendulum
        parameter Real M = 1.2 "台車の重量";
        parameter Real m = 0.3 "棒の重量";
        parameter Real l = 0.8 "棒の長さ";
        constant Real g = 9.81 "重力加速度";
        Real x (start=0);
        Real v;
        Real theta (start=0.01);
        Real vtheta;
        input Real F;
    equation
        v=der(x);
        vtheta=der(theta);
        (M+m)*der(v) - m*l*der(vtheta)*cos(theta) + m*l*vtheta^2*sin(theta) = F;
        l*der(vtheta) - g*sin(theta) = der(v) *cos(theta);
        
    end Pendulum;

end InvertedPendulum;

このファイルをJuliaから実行してシミュレーションします。

Juliaファイル

Julia言語で上記modelicaファイルを実行します。また、今回はアニメーションも作成します。アニメーションの作成方法は以下の記事を参照してください。

otepipi.hatenablog.com

今回は外力はなし(F=0)でシミュレーションします。

using Plots
using OMJulia
using Interact

pen = OMJulia.OMCSession();
pen.ModelicaSystem("InvertedPendulum.mo","InvertedPendulum.Pendulum");

pen.setSimulationOptions(["stopTime=7"]);
pen.setInputs("F = 0")
pen.simulate();
tm,x,θ = pen.getSolutions(["time","x","theta"]);
par = pen.getParameters();
len = parse(Float64,par["l"]);
simsize = size(tm);

 xp = x.-len.*sin.(θ);
 yp = len.*cos.(θ);

 verts = [(-1, 0), (1, 0), (1, -1),(0.8,-1),(0.8,-1.2),(0.6,-1.2),
        (0.6,-1.0),(-0.6,-1.0),(-0.6,-1.2),(-0.8,-1.2),(-0.8,-1),(-1,-1)] ;

@gif for i in 1:10:simsize[1]
scatter([x[i],xp[i]],[0,yp[i]],markershape =[Shape(verts),:circle],markersize = [100,15],
xlims = (-1, 1),ylims =(-1,1),
title="time=$(tm[i])s",size=(500,500),leg = false,showaxis = :off)

plot!([x[i],xp[i]],[0,yp[i]],lw=10)
end

今回以下の構文で台車（のような）形状のマーカーを新規に作成しています。

 verts = [(-1, 0), (1, 0), (1, -1),(0.8,-1),(0.8,-1.2),(0.6,-1.2),
        (0.6,-1.0),(-0.6,-1.0),(-0.6,-1.2),(-0.8,-1.2),(-0.8,-1),(-1,-1)] ;

結果、以下のようなアニメーションを得ることができました。

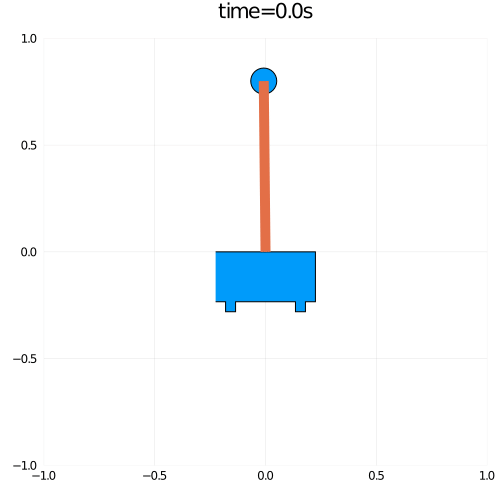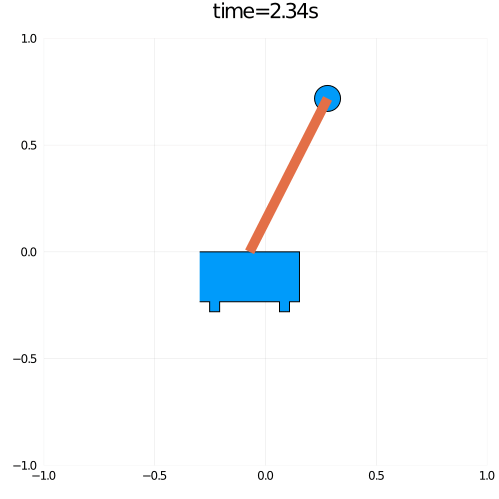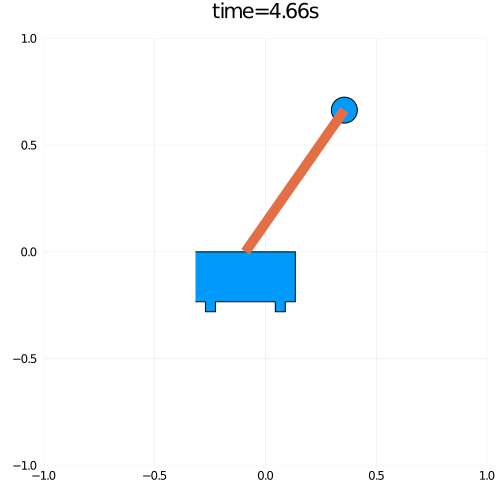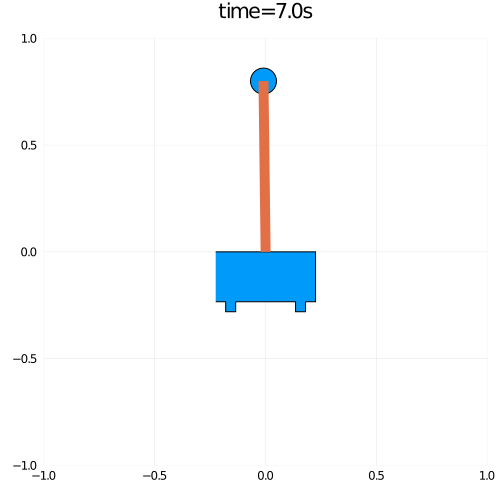
f:id:Otepipi:20210211202648g:plain

短いですが今回はここまでにします。

システムとモデリング

modelica, Julia, Design Structure Matrix, SysML, 他モデリング全般について。

【Julia言語入門】Juliaとmodelicaで倒立振子のアニメーション

倒立振子のモデル

modelicaファイル

Juliaファイル