これまで何回かJuliaでPID制御をする記事を書きましたが、コードの正しさを確認する検定を行っていなかったので今回はそれを確認します。
過去の記事は以下
今回の検定内容
ジーグラス・ニコルス法によるステップ応答によるPID自動調整のプログラムが正しいか確認します。
例題
以下の書籍から例題を引っ張ってきています。

- 作者: システム制御情報学会
- 出版社/メーカー: 朝倉書店
- 発売日: 1992/07/01
- メディア: 単行本
- 購入: 1人 クリック: 5回
- この商品を含むブログ (1件) を見る
以下の伝達関数を持つ1次遅れ・むだ時間系のPID定数をジーグラ・ニコルス法で求めます。 $$ G = \frac{1}{1+1.0925 s} e^{- s} $$ この伝達関数のステップ応答を逆ラプラス変換すると以下のようになります。
$$ y = 1- e^{-0.91533(t - 1)} $$
なお、先述した教科書によりますとこのときのPIDパラメーターは以下になります。
Kp = 1.311 Ti = 2 Td = 0.5
Juliaでの実装
Juliaでジーグラ・ニコルス法のPIDパラメーターを求めるプログラムは以下になります。
using Plots using LinearAlgebra tm = 1000 #シミュレーションステップ数 st = 0.01 #1ステップあたりの時間 # 空の配列の作成 y_ = zeros(tm + 1) for t in 0:tm if t < 100 y = 0 else y = 1 - exp(-0.91533*(t*st-1)) end y_[t+1] = y end # 傾斜の最も大きな値を探すため、差分をとる。 #差分行列の作成 dv = ones(tm + 1) ev = -1 *ones(tm) A = Bidiagonal(dv,ev, :L) A[1,:] = zeros(1,tm+1) ⊿y = A * y_ #最大値とそのインデックス maxb,indexb = findmax(⊿y) #最大接線の式 maxy = y_[indexb] cons = maxy - maxb * indexb #式は y = maxb * x + con yda = maxb .* (0:250) + cons .* ones(251) p = plot([0:st:tm*st],[y_],title="STEP",label=["y"]) plot!([0:st:250*st],[yda]) display(p) R = maxb L = -1 * cons / maxb Kp = 1.2/(R*L) Ti = 2*L*st Td = 0.5*L*st println("Kp=",Kp,"Ti=",Ti,"Td=",Td)
グラフは以下になります。
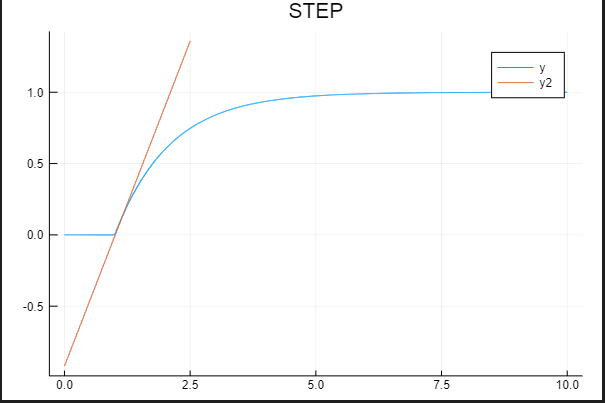
また、このプログラムではPIDパラメーターは以下のようになります。
Kp = 1.304 Ti = 2.02 Td= 0.505
わずかに誤差はありましたが、ほぼ教科書通りの値になることがわかりました。
今回はここまでにします。