【Julia入門】Juliaで一次元のセルオートマトンを描画する

今回はシステムの離散モデルの1種であるセルオートマトンをJuliaで描画してみたいと思います。

最近、『東京大学工学教程　システム工学』シリーズを読む機会がありました。

作者:大橋弘忠,古田一雄
発売日: 2015/06/15
メディア: 単行本（ソフトカバー）

作者:大橋弘忠,鳥海不二夫,白山晋
発売日: 2016/09/29
メディア: 単行本（ソフトカバー）

システムのモデリング手法（常微分方程式、離散モデル、ネットワーク、確率モデル）について概要を広く学べる内容でとても参考になりました。離散モデルの１つにオートマトンが紹介されていたのですが、そういえば自分では一度も実装したことが無かったので、これを機にJuliaでシミュレーションしてみようと考えました。

上記書籍には実装コードまでは載っていなかったので、Pythonのコードが掲載されている下記書籍を参考にしました。

作って動かすALife ―実装を通した人工生命モデル理論入門

作者:岡瑞起,池上高志,ドミニク・チェン,青木竜太,丸山典宏
発売日: 2018/07/28
メディア: 単行本（ソフトカバー）

一次元セルオートマトンとは

セルオートマトンは下のように四角いセルが一次元に配列されたものを指します。

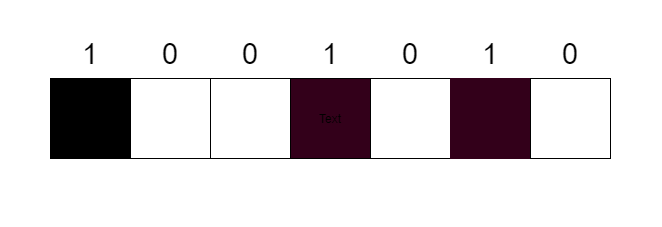
f:id:Otepipi:20200922202622p:plain

このセルひとつひとつは「１(黒塗り）」と「０（白塗り）」の２つの状態を持ちます。そしてこれらのセルはそれぞれ時間ステップとともに状態を変えていきます。『自身とその両隣のセル』の状態により、次のタイムステップでの状態を決定する場合が多いです。下図のように、自身とその両隣の0と1により、次の自分の状態が決まります。

f:id:Otepipi:20200922203326p:plain

このとき、3セルの状態は000から111まで計8通りあります。そのそれぞれについて、自身の次の状態が0か1かの2通りありますので状態を決めるルールは2⁸=256通りあります。

今回、シミュレーションではルール30についてまず実施してみます。

f:id:Otepipi:20200922203816p:plain

セル・オートマトン - Wikipedia

このルール30の「30」がどこから来ているのかというと、上記画像の「中央のセルの次の状態」の2進数00011110を10進数になおすと「30」になることからです。この命名則はプログラミングする上でもとても便利な法則になっています。

一次元セルオートマトンの実装

まずセルの数を10個、タイムステップを10としたコードを作成してみます。

using LinearAlgebra
using Plots

RULE=30;
SPACE_SIZE=10;
TIME_STEP=10;

global state = zeros(SPACE_SIZE);
global next_state = zeros(SPACE_SIZE);
global state_time = zeros(TIME_STEP,SPACE_SIZE);

###　初期条件 中央の1ピクセルのみ１
state[length(state)÷2] = 1

#stateの評価
for time = 1:TIME_STEP

for i = 1:SPACE_SIZE
    l = state[if i > 1 i-1 else SPACE_SIZE end]
    c = state[i]
    r = state[i % SPACE_SIZE + 1]
    neighbor_cell_code = Int(2^2*l + 2^1*c + 2^0*r) 

    if RULE >> neighbor_cell_code & 1 > 0
        next_state[i] = 1;
    else
        next_state[i] = 0;
    end
end
state_time[time,:] = state[:]
state[:] = next_state[:]
end

## 描画
heatmap(state_time, yflip = true, c = :heat, legend = false,
        ylabel="time step")